航空機と自動車の品質マネジメントシステムの要求の違い 第7回

前回は、統計的工程管理(SPC)のうち、管理図の話をいたしましたが、今回は、工程能力を取り上げます。
工程能力の評価
次に工程能力の評価ですが、生産数量が多いと工程の安定性を評価する工程能力指数(要求公差幅に対して加工の平均値のずれとばらつきを評価)を算出することができます。図面で要求されるその個所の寸法の許容公差に対して、現在の加工方法で得られるデータがどのように分布しており、公差を外れる危険性がどれだけあるかが計算上得られるものです。(この例では、平均値が公差の中央値に等しいケースで示します)
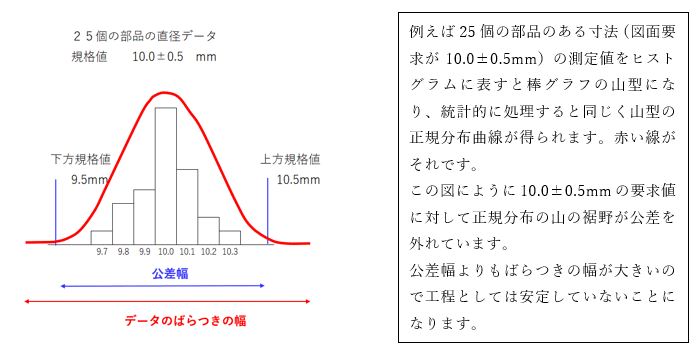
この時の工程能力指数(Cp)は、Cp=公差幅/データのばらつきの幅で計算でき、この分布で公差幅が10.0±0.5mmで図のような分布の場合は、Cp=0.79になります。一般的には、Cpが1.33以上あると工程能力があるなどと評価されます。因みにCp=1.0の時の公差を外れる確率は、0.3%になり、不合格率も推定できます。
ばらつきの形は統計的に処理した際に正規分布で近似できるといいましたが、実は、正規分布を計算の際に同時に計算で得られるばらつきの指標があり、標準偏差(S)といいます。統計的には、ばらつきのすそ野の幅は、標準偏差の6倍になるといわれています。
従って、統計的にはデータのばらつき幅=6x Sとなります。Cp=公差幅/6 x Sで計算できます。
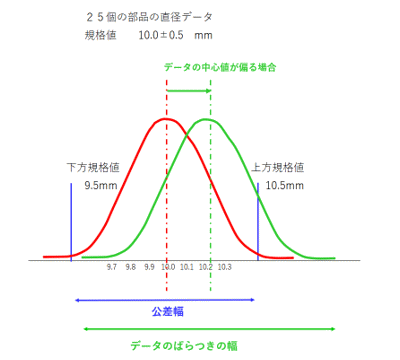
ところで実際のデータは、必ずしも先の例のように公差の中央値とデータの分布の平均値が一致しないので下図の緑の分布のように偏りが出ます。
この偏った分だけ工程能力が落ちることになり、この偏りを加味した工程能力指数を計算することができます。これをCpkと言っています。
緑の分布の平均値が10.2mmとしますと、偏り率(K)は(公差中央値からのずれ量:0.2mm)/(公差幅の半分:0.5mm)で求められ、40%になります。Cpk=Cp x (1-K)=0.79 x (1-0.4)=0.47となります。分布の平均値がずれた分だけ工程能力も落ちたわけです。
お分かりになりましたでしょうか? 統計は、トラブルシューティングなどでも幅広く活用されています。興味のある方は、是非解説本を手にして学んでいただきたいを思います。
文責 山本 晴久
「続き(第8回)を読む」
【e-learning】航空機の品質保証 ~自動車との比較理解~
航空機の品質保証の特徴や勘所について、航空宇宙製品に適用されている規格のAS9100の特徴と、自動車の品質保証を
比較しながら解説するオンライン学習を販売しております。
好きな時間に自分のタイミングで受講頂けます。興味のある方は、是非サンプルも試聴することができますので、
お気軽にお問合せ下さい。
