今回は散布図について説明いたします。散布図は、一対になったデータの相互の関係を取り扱います。最初に実際の例で見てみましょう。

両面テープの圧着時間と接着力を一対のデータとして取得したものを表－１に示します。また、その結果からX軸に圧着時間、Y軸に接着力を点で記入したものを図－１に示します。
図－１から、各点は、左下から右上に右上がりの形で分布しています。これは、圧着時間が長くなるほど接着力も強くなることを示しています。

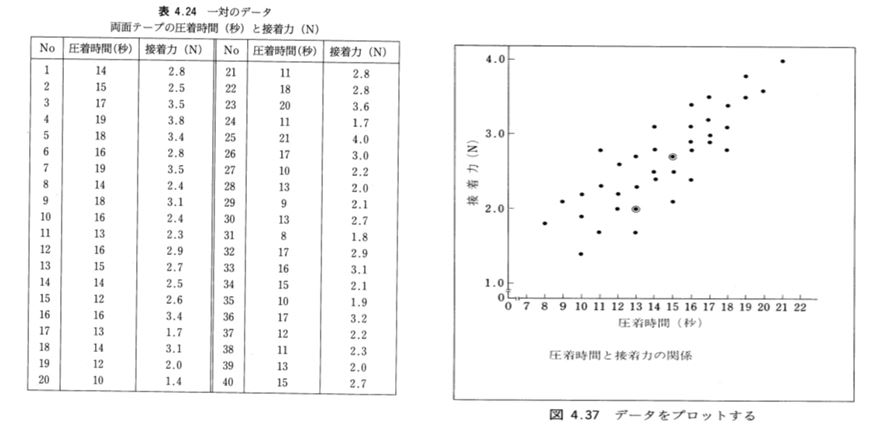
このように2つのパラメータの相互の関係を把握したい時にこの相関図を使います。
上記の例は、正の相関といいます。

また、塗装工程があり乾燥温度が高いと母材に密着し不良は出ないが、温度が低いと密着が弱く不良率が上がる工程で、いくつかの乾燥温度を縦軸に、密着度の不良率のデータを横軸にプロットすれば、先の右上がりでなく、右下がりの分布になるでしょう(図は省略します）。これを負の相関と言っています。

このように相関図を作ることで一対のデータの相互の関係を掴むことができます。散布図の一般的な見方を下図に示します。

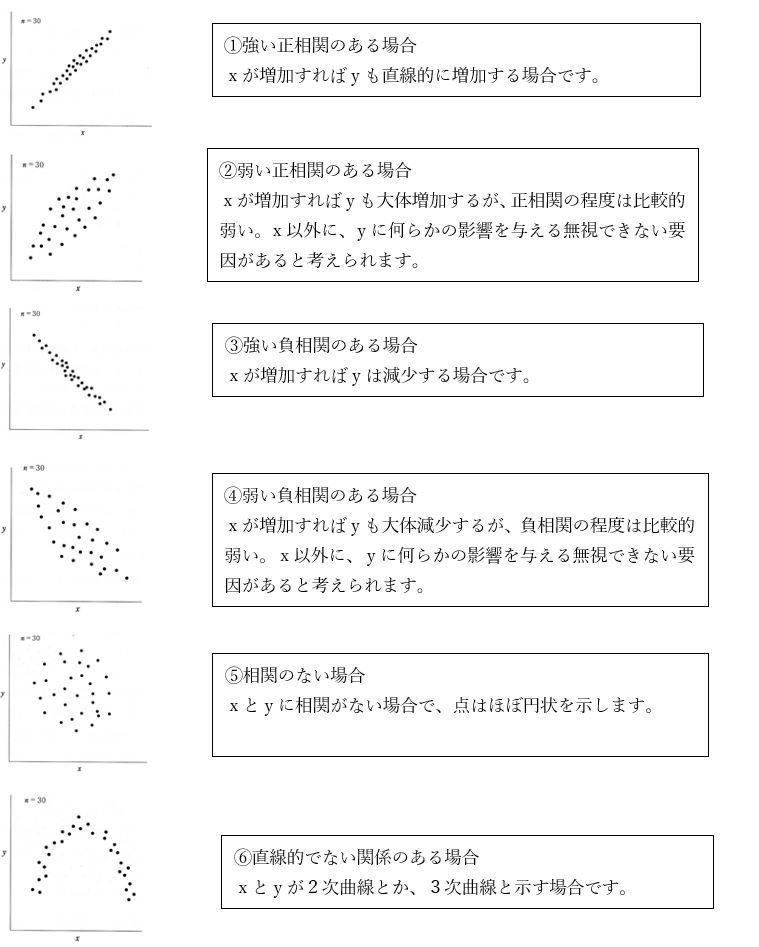
散布図の分布でおおよその相関係数がわかります。右上がりに一直線に乗る場合は、正の相関で相関係数r=１で、右下がりに一直線に乗るものは、負の相関で相関係数ｒ＝－１で、プロットした点が一様に大きく広がり相関が全くなければｒ＝０となります。相関係数は、１から－1までの数値をとります。

因みに相関係数の目安の面白いデータがありましたので下記に紹介します。

相関係数は、7つ道具ではありませんが、散布図との関連が深いためここで紹介させていただきました。
次回は、管理図の解説で、このシリーズの締めくくりになります。

文責　山本晴久

「続き（第９回）を読む」

　当社では主に航空宇宙の品質に関わるご支援をしております。
　以下、リンクです。
・JIS Q 9100:2016 認証取得支援
・Nadcap 認証取得・更新支援
・JIS Q 9100:2016 規格解説セミナー
・JIS Q 9100:2016 内部監査員養成セミナー
・その他、お気軽にお問合せください。

名古屋品証研株式会社